Trigonometric Functions of Any Angle

• Examples
• Definitions of the Trigonometric Functions of Any Angle
• Example
• The Unit Circle
• Exercise 1
• Exercise 2
• Exercise 3
• Exercise 4
• Exercise 5
• Exercise 6
• Exercise 7
• Example 8
• Example 9
• Example 10

S. F. Ellermeyer

Examples

Definitions of the Trigonometric Functions of Any Angle

Example

The Unit Circle

The unit circle should be memorized. The best way to memorize it is to study and understand  it.

Exercise 1

In which quadrant do angles of the following measure lie?

1. -14.3 degrees

2. -120 degrees

3. 1075 degrees

4. 315 degrees

5. -58,000 degrees

Exercise 2

1. Find two positive angles and two negative angles that are coterminal with -81 degrees.

2. Find two positive angles and two negative angles that are coterminal with 250 degrees.

Exercise 3

1. Find the complement and the supplement of 47 degrees.

2. Find the complement and the supplement of 9.038 degrees.

Exercise 4

Find the six trigonometric function values for the angle pictured below.

Exercise 5

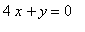Given that the terminal side of angle  lies on the line  in quadrant II, find the six trigonometric function values of .

Exercise 6

Given that 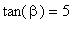 and that the terminal side of  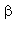lies in quadrant I, find the other five trigonometric function values of .

Exercise 7

For each of the angles given below, find the reference angle and find the exact trigonometric function

values if possible.

1. -225 degrees

2. 855 degrees

3. -135 degrees

Example 8

Find the signs of the six trigonometric function values of the following angles.

1. -57 degrees

2. -620 degrees

3. 91 degrees

Example 9

Given that

use a calculator to find find the trigonometric function values for 333 degrees. However, do not use the trigonometric function keys on the calculator.

Example 10

1. Given that 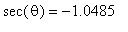 and that  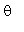is between 90 and 180 degrees, find the approximate value of   .

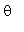2. Given that 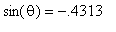 and that  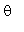is between 180 and 270 degrees, find the approximate value of .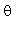